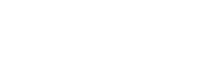مجموع قياسات الزوايا الداخلية للمضلع السداسي
جدول المحتويات
مجموع قياسات الزوايا الداخلية للمضلع السداسي تكون عبارة عن مجموع مقدار الزوايا الستة للمضلع السداسي، حيث يعد الشكل السداسي أحد الأشكال الهندسية، والتي يطبق عليها قوانين المساحة والمحيط وقوانين الزوايا، وفي هذا المقال سنتحدث بالتفصيل عن سداسي الأضلاع، وسنوضح كم مجموع قياسات زواياه.
ما هو سداسي الأضلاع
سداسي الأضلاع (بالإنجليزية: Hexagon)، هو شكل من الأشكال الهندسية والرياضية، وهو عبارة عن ست أضلاع متساوية في المضلع السداسي المنتظم، كما ويكون له ست زوايا متماثلة في المضلع المنتظم، حيث أنه عندما يكون طول جميع الأضلاع وجميع الزوايا متساوية، يكون شكل السداسي منتظم، وإن لم تكن متساوية يكون السداسي غير منتظم، وفي الواقع إن الشكل السداسي يتواجد بكثرة في الطبيعة وذلك بسبب طريقة تشابكه، وأقرب مثال عليه هو خلية النحل التي تكون عبارة عن أشكال سداسية متتطابقة ومبنية فوق بعضها البعض، وهذا هو ما يميز الشكل السداسي عن غيره من الأشكال الهندسية، وهو التطابق عند بناء هذه الأشكال الهندسية فوق بعضها.[1]
مجموع قياسات الزوايا الداخلية للمضلع السداسي
إن مجموع قياسات الزوايا الداخلية للمضلع السداسي هي 720 درجة، حيث إن الشكل السداسي المنتظم يمتلك ست زوايا، ومقدار كل زواية من هذه الزوايا هو 120 درجة، كما وإن نصف قطر الدائرة المحيطة بالسداسي المنتظم تساوي طول أحد أضلاعه، ولكن إن الشكل السداسي غير المنتظم لا يكون مقدار زواياه 120 درجة وإنما تختلف بإختلاف أبعاد الشكل المضلع، ولكن يبقى مجموع زواياه هو 720 درجة، ويمكن صياغة مجموع زوايا السداسي غير المنتظم بالقانون الأتي:[2]
مجموع زوايا سداسي الأضلاع = الزاوية 1+ الزاوية 2 + الزاوية 3 + الزاوية 4 + الزاوية 5 + الزاوية 6
720 درجة = «ز1 + «ز2 + «ز3 + «ز4 + «ز5 + «ز6
إذا كان الشكل السداسي له زوايا خمسة معروفة فقط، وزاوية واحدة مجهولة، فيمكن حساب الزاوية المجهولة بهذا القانون، وعلى سبيل المثال، لو كان مضلع سداسي يمتلك الزوايا الخمسة التالية على الترتيب، 36 درجة، 25 درجة، 105 درجة، 180 درجة، 150 درجة، فيمكن حساب الزاوية المجهولة بهذه الطريقة التالية:
مجموع زوايا سداسي الأضلاع = الزاوية 1+ الزاوية 2 + الزاوية 3 + الزاوية 4 + الزاوية 5 + الزاوية 6
720 درجة = «ز1 + «ز2 + «ز3 + «ز4 + «ز5 + «ز6
720 درجة = 36° + 25° + 105° + 180° + 150° + «ز6
«ز6 = 720° – 36° + 25° + 105° + 180° + 150°
«ز6 = 224°
الزاوية السادسة = 224 درجة
مساحة المضلع السداسي المنتظم
يمكن حساب مساحة المضلع السداسي المنتظم فقط، وذلك من خلال القوانين والصيغ الرياضية والتي تعتمد على مقدار طول ضلع الشكل السداسي، حيث إن ضرب 2.598 بطول الضلع تربيع سيعطي مساحة المضلع السداسي، وعلى سبيل المثال لحساب مساحة مضلع سداسي منتظم طول ضلعه يساوي 4 سنتيمتر، تكون طريقة إيجاد المساحة كالأتي:[3]
مساحة المضلع السداسي = 2.598 × مربع طول الضلع
م = 2.598 × ض²
حيث إن م هي مساحة المضلع، وض هي طول الضلع:
م = 2.598 × ²4
م = 41.568 سم²
كما ويمكن حساب محيط الضلع السداسي، وذلك من خلال جمع أطوال أضلاع السداسي، وإذا أردنا حساب محيط الشكل السداسي في المثال السابق، فتكون طريقة إيجاد المحيط كالأتي:
محيط المضلع السداسي = مجموع أضلاع السداسي
وبما أن طول أضلاع السداسي منتظمة ومتساوية، ويبلغ عددها ست أضلاع فينتج:
محيط السداسي = طول الضلع × 6
ح = ض × 6
حيث إن ح هو محيط السداسي، و ض هو طول الضلع:
ح = 4 × 6
ح = 24 سم
وفي ختام هذا المقال نكون قد عرفنا أن مجموع قياسات الزوايا الداخلية للمضلع السداسي تساوي 720 درجة، كما ووضحنا ما هو المضلع السداسي، وذكرنا أنواعه سواء النوع المنتظم أو النوع غير المنتظم، كما وشرحنا طريقة حساب مساحة السداسي المنتظم وطريقة حساب محيطه.